Daniel A. Fisch

Daniel A. Fisch

I am an Economist and Theoretical Physicist with a master's degree in Economics, from BSE (2024), and in Applied Mathematics, from the University of Cambridge (2023).

Predicting Opinion Phases in the Hegselmann-Krause Model

2 minute read

The code for this project is available on my GitHub.

In simple terms, the research field of opinion dynamics asks: Given an initial opinion state $x(0)$ and dynamics specified by a set of (general) interaction rules on a network, what can be said about the final behavior of the opinion profile, i.e. $\lim\limits_{t \to \infty} x(t)$? In particular, when is consensus $c$ reached, i.e. $\forall i = 1,\dots,N$: $\lim\limits_{t \to \infty} x_i(t) \equiv c$?

In order to address the diversity of the research area of opinion dynamics, I gave a general overview of different types of models within the applied area of opinion dynamics, combining different types of updating rules, interaction networks, deterministic and stochastic dynamics (e.g. the voter, DeGroot and Hegselmann-Krause (HK) model). In addition, I used simple examples to illustrate two relevant mathematical concepts in opinion dynamics: the extra effort involved in sequential updating due to randomness and the network structure of agents, which is particularly relevant for simultaneous updating.


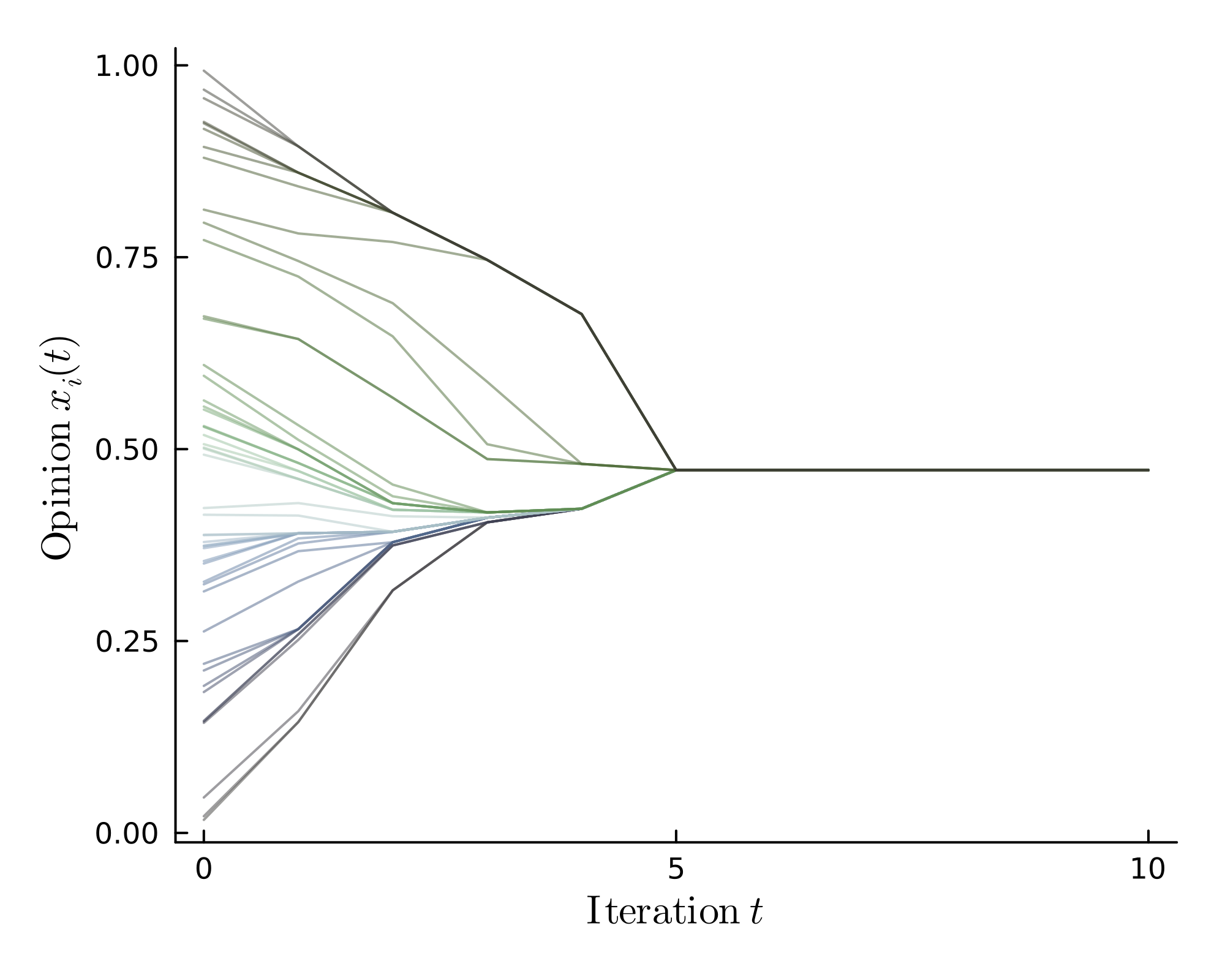
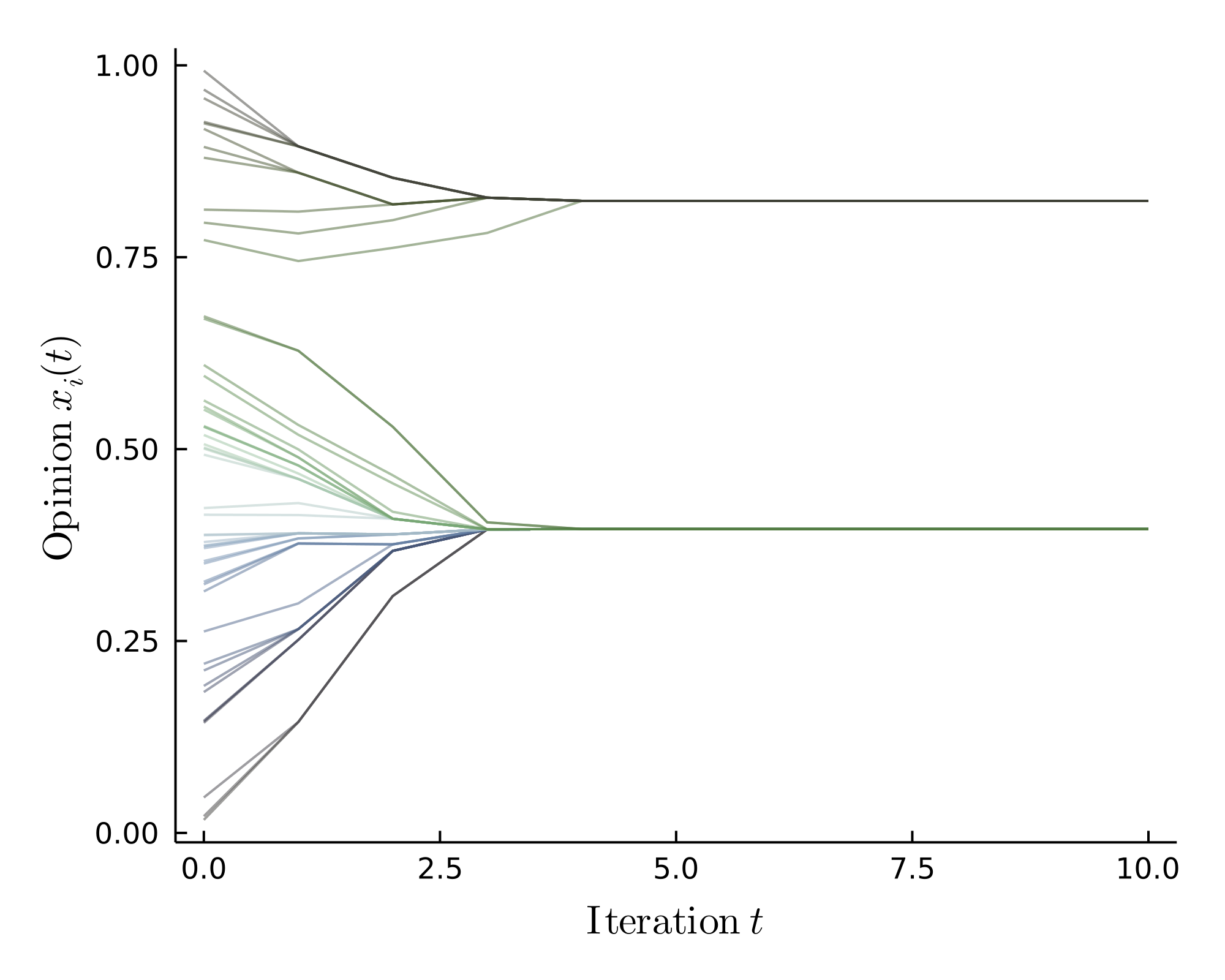
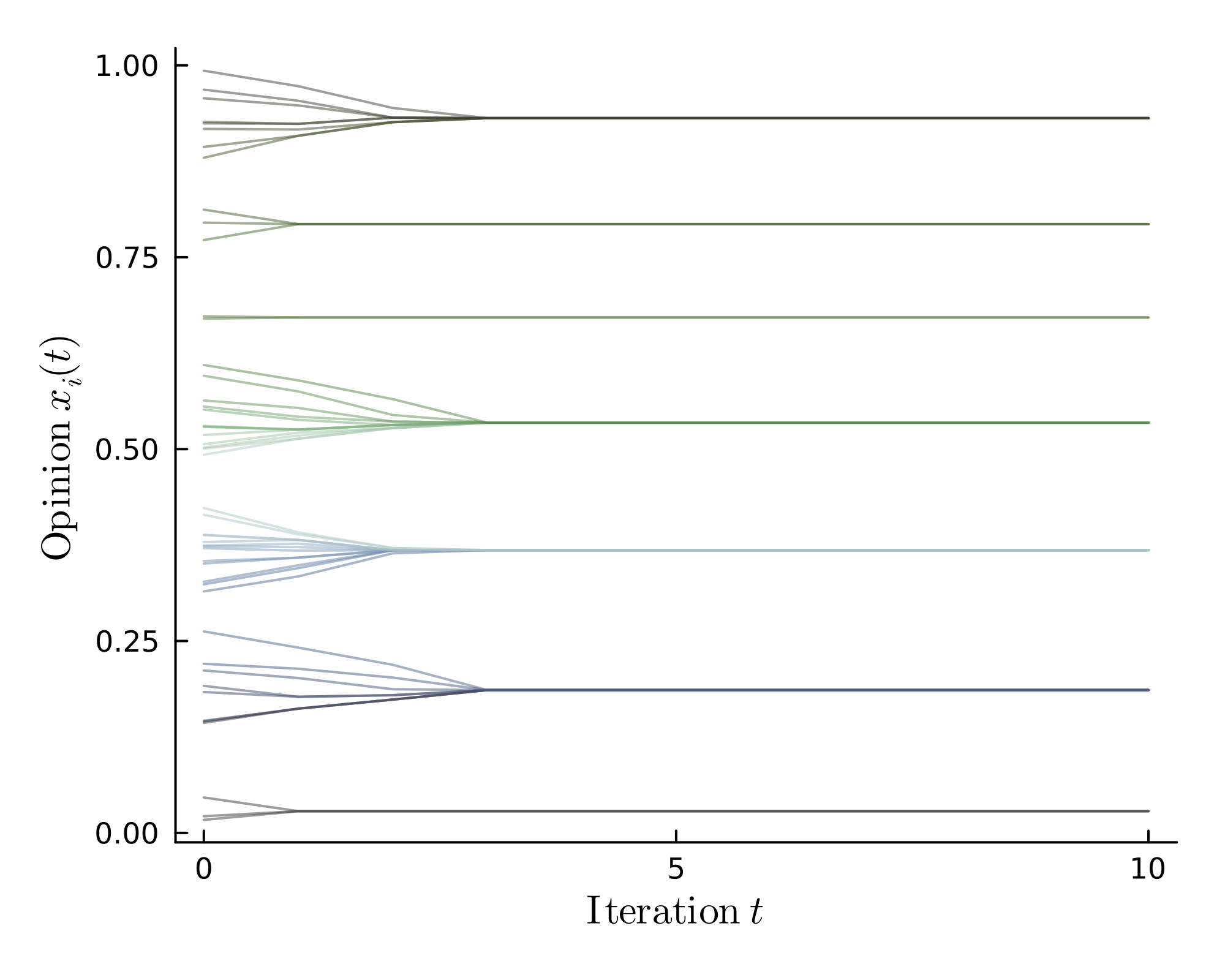
The different opinion phases of the HK model: consensus, polarization and fragmentation.

I then delved deeper into the non-linear HK bounded confidence model with the three opinion phases: consensus, polarization and fragmentation. It is possible to gain some fundamental insights using analytical methods, yet other phenomena are better investigated using computer simulations. The HK model operates according to the principle that dense regions have a stronger influence on less dense ones in their vicinity as seen in the polarized phase, i.e. a (local) majority shapes opinion formation, which makes intuitively sense. Using stability analysis, it was possible understand the number of different clusters emerging from the HK model in the fragmented phase better. This improves the theoretical estimate for the number of clusters from $\frac{1}{\varepsilon} \rightarrow \frac{1}{2\varepsilon}$, which is much closer to simulation results. I also looked at alterations of the original model. Introducing a small noise leads to quasi-consensus after long enough times. However, a too large noise renders quasi-consensus impossible since opinion clusters can split off and (at least temporarily) continue to evolve independently.


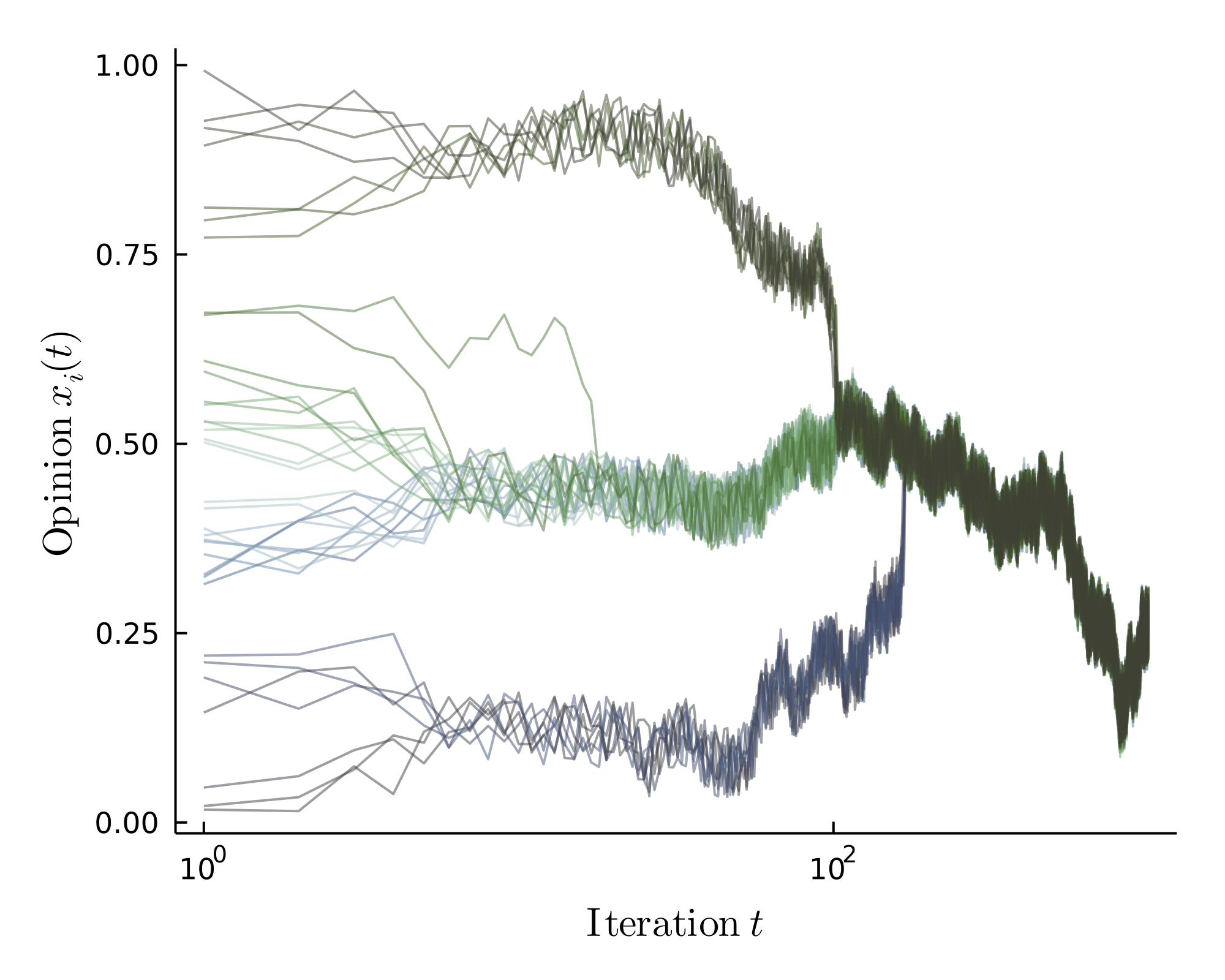
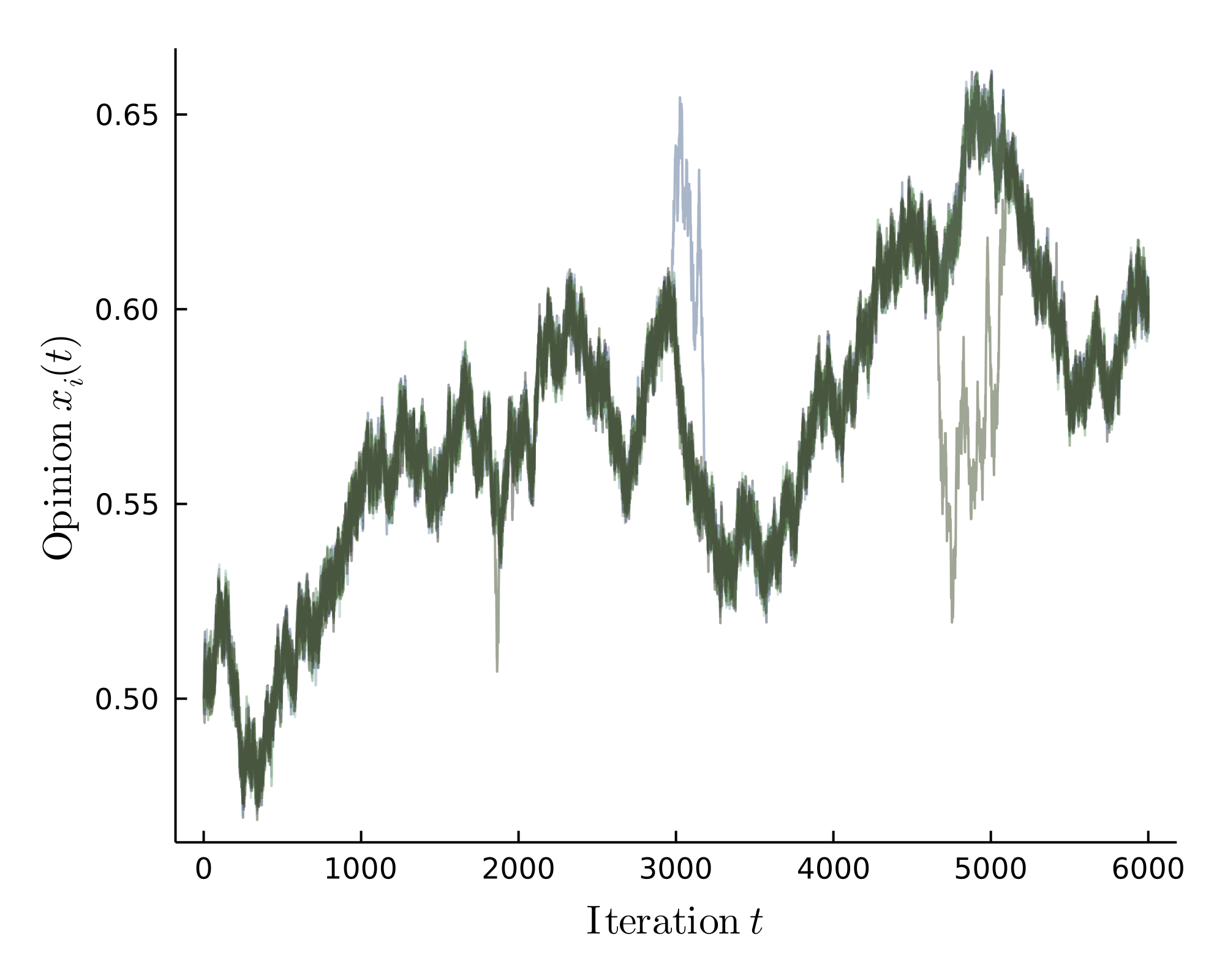
Small noise leads to quasi-consensus. However, large noise leads to temporary cluster formation.

The mathematical methods involved are probability theory, linear algebra, stochastic processes, PDEs, mean-field approximations and computing.